算法基本概念

什么是算法

算法(Algorithm)是对特定问题求解步骤的一种描述，它是指令的有限序列，其中的每条指令表示一个或多个操作。

算法还具有下列 5 个重要特性：

1. 有穷性

   一个算法必须总在执行有穷步之后结束，且每一步都可在有穷时间（合理的，可接受的）内完成。

   算法必须是有穷的，程序既可以是有穷的也可以是无穷的

2. 确定性

   算法中每条指令必须有确切的含义，对于相同的输入只能得出相同的输出。

3. 可行性

   算法中描述的操作都可以通过已经实现的基本运算执行有限次来实现。

4. 输入

   一个算法有零个或多个输入，这些输入取自于某个特定的对象的集合。

5. 输出

   一个算法有一个或多个输出，这些输出是与输入有着某种特定关系的量

“好”算法设计的要求

1. 正确性

   算法应能够正确地解决求解问题。

   如果算法不能正确解决问题，那么这个算法不是一个好算法，但也能被称为算法。

2. 可读性

   算法应具有良好的可读性，以帮助人们理解。

3. 健壮性

   输入非法数据时，算法能适当地做出反应或进行处理，而不会产生莫名其妙的 输出结果。

4. 高效率与低存储量需求

   效率是指算法执行的时间，高效率即花的时间少、时间复杂度低；存储量需求是指算法执行过程中所需要的最大存储空间，低存储量需求即不费内存、空间复杂度低；这两者都与问题的规模有关。

算法效率的度量

算法效率的度量是通过时间复杂度和空间复杂度来描述的。

时间复杂度

一个语句的频度是指该语句在算法中被重复执行的次数。

算法中所有语句的频度之和记为 $T(n)$，它是该算法问题规模 $n$ 的函数，时间复杂度主要分析 $T(n)$的数量级。

算法中基本运算（最深层循环内的语句）的频度与 $T(n)$ 同数量级，因此通常采用算法中基本运算的频度 $f(n)$ 来分析算法的时间复杂度。因此，算法的时间复杂度记为

$$T(n)=O(f(n))$$

式中，$O$ 的含义是 $T(n)$ 的数量级，其严格的数学定义是：若 $T(n)$ 和 $f(n)$是定义在正整数集合上的两个函数，则存在正常数 $C$ 和 $n_0$，使得当 $n$ ≥ $n_0$ 时，都满足 $0$ ≤ $T(n)$ ≤ $Cf(n)$。

在分析一个程序的时间复杂性时，有以下两条规则：

1. 加法规则 多项相加，只保留最高阶的项，且系数变为 1

   $$T(n)=T_1(n)+T_2(n)=O(f(n))+O(g(n))=O(max(f(n),g(n)))$$

   操作数量 $T(n)$	时间复杂度 $O(f(n))$
   10000000	$O(1)$
   $3n+2$	$O(n)$
   $2n^2+3n+2$	$O(n^2)$
   $n^3+10000n^2$	$O(n^3)$
   $2^n+10000n^{100000}$	$O(2^n)$

2. 乘法规则

   多项相乘，都保留

   $$T(n)=T_1(n)\times T_2(n)=O(f(n))\times O(g(n))=O(f(n)\times g(n))$$

常见的渐近时间复杂度为

$$0(1)<O({\log }_{2}n)<O(n)<O(n{\log }_{2}n)<O(n^2)<O(n^3)<0(2^n)<0(n!)<O(n^n)$$

常数阶 $O(1)$

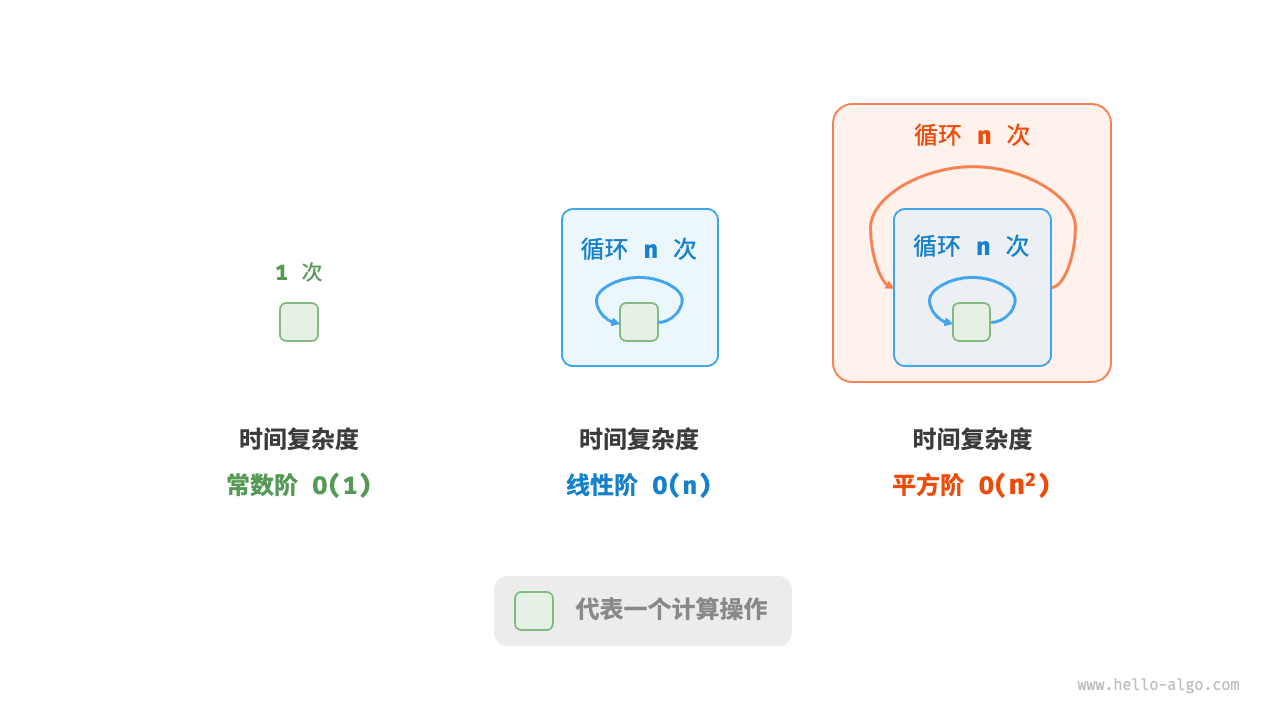
常数阶的操作数量与输入数据大小 $n$ 无关，即不随着 $n$ 的变化而变化。

线性阶 $O(n)$

线性阶的操作数量相对于输入数据大小以线性级别增长。线性阶通常出现在单层循环中。

平方阶 $O(n^2)$

平方阶的操作数量相对于输入数据大小以平方级别增长。平方阶通常出现在嵌套循环中，外层循环和内层循环都为 $O(n)$，因此总体为$O(n^2)$。

指数阶 $O(2^n)$

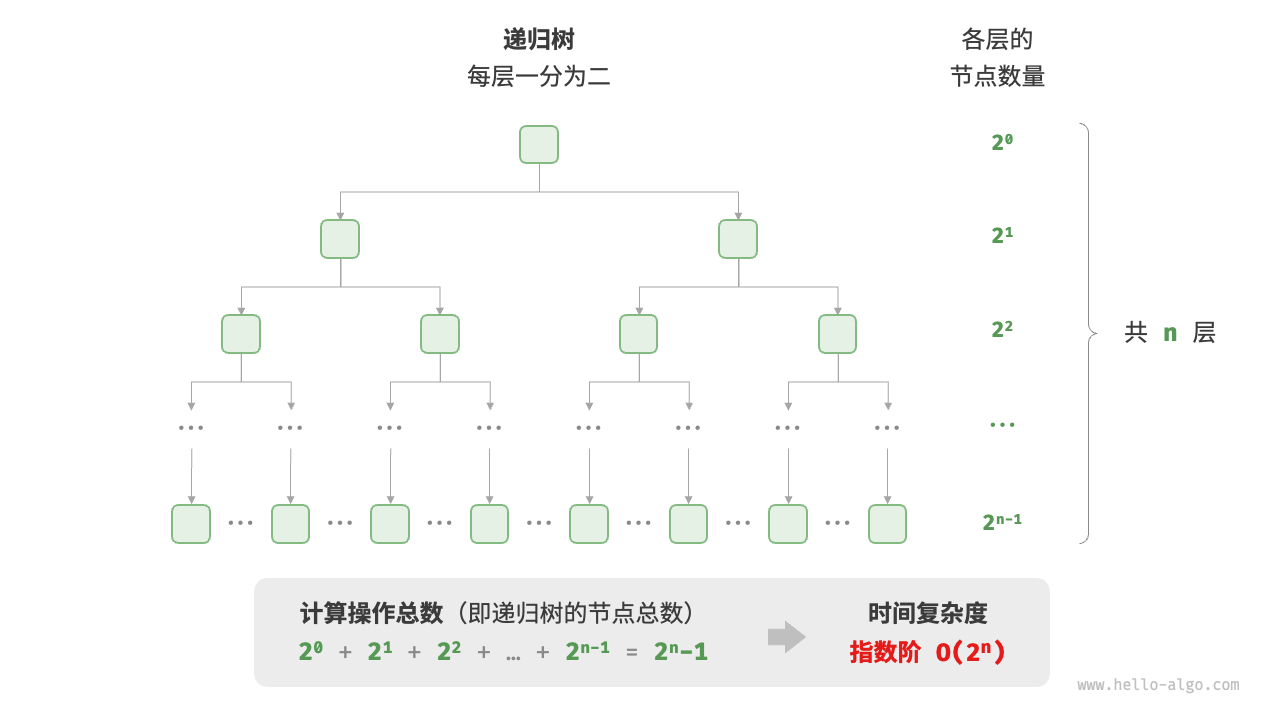
指数阶增长非常迅速，在实际应用中通常是不可接受的。若一个问题使用「暴力枚举」求解的时间复杂度为 $O(2^n)$，那么通常需要使用「动态规划」或「贪心算法」等方法来解决。在实际算法中，指数阶常出现于递归函数。

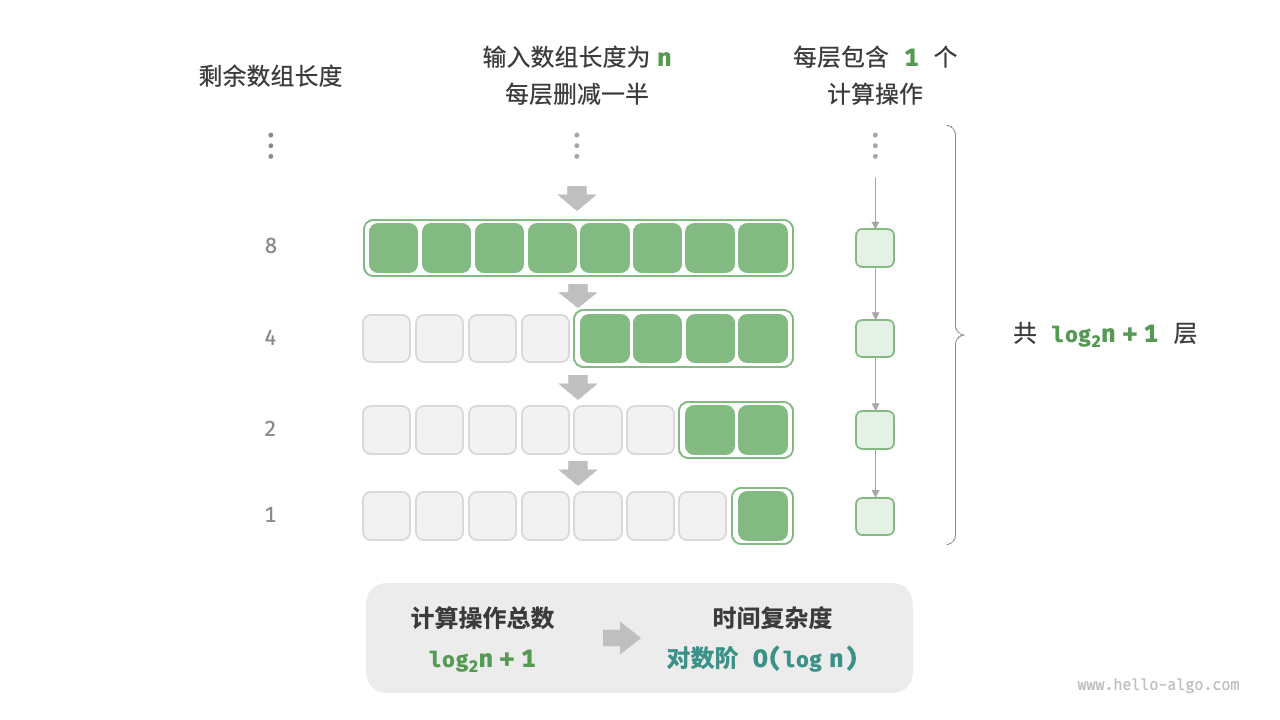
对数阶 $O(\log (n))$

对数阶仅次于常数阶，时间增长缓慢，是理想的时间复杂度。对数阶常出现于「二分查找」和「分治算法」中，体现了“一分为多”和“化繁为简”的算法思想。

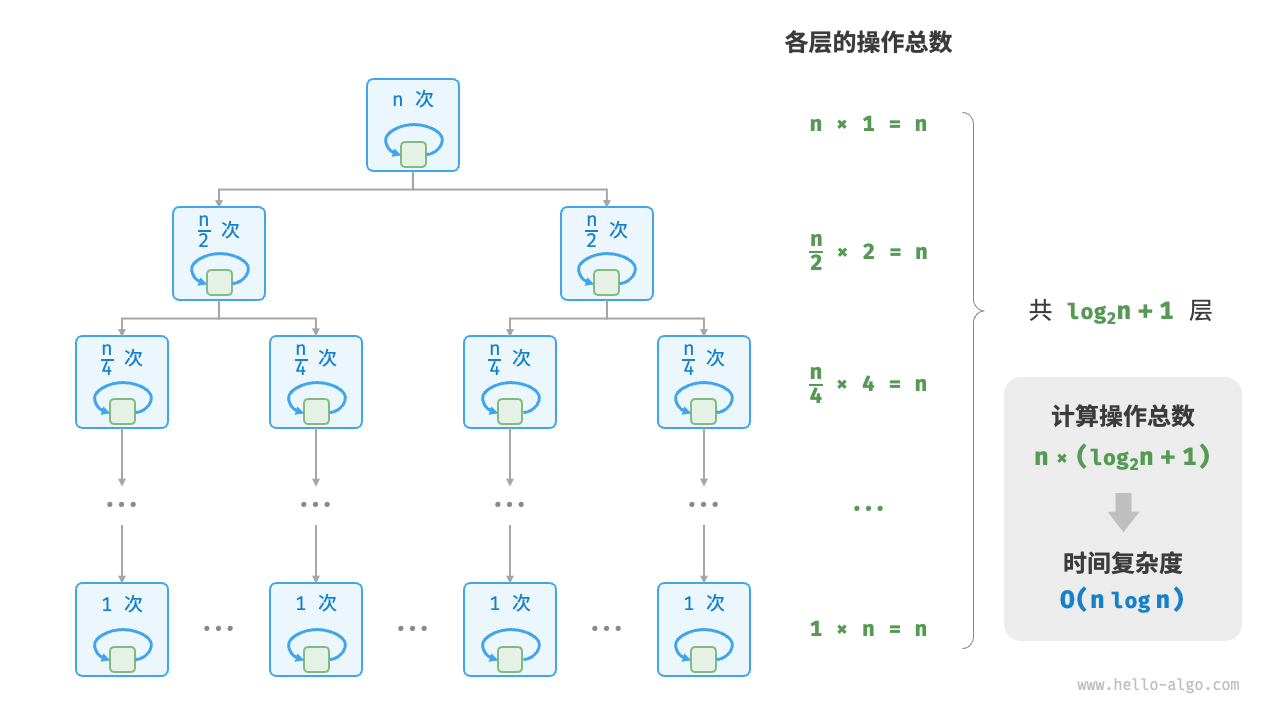
线性对数阶 $O(n\log (n))$

线性对数阶常出现于嵌套循环中，两层循环的时间复杂度分别为 $O(\log (n))$和 $O(n)$。

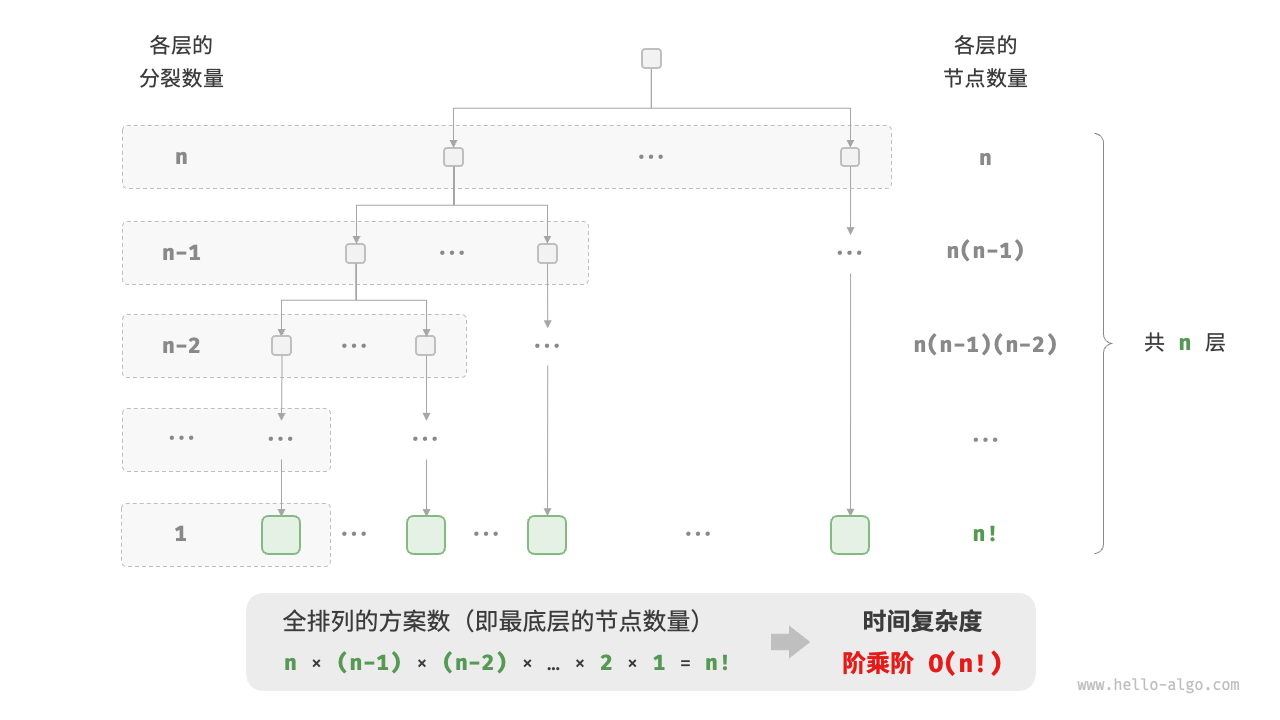
阶乘阶 $O(n!)$

阶乘通常使用递归实现。

最差、最佳、平均时间复杂度

算法的时间复杂度不仅依赖于问题的规模 n，也取决于待输入数据的性质。

• 最坏时间复杂度：在最坏情况下，算法的时间复杂度。
• 平均时间复杂度：所有可能输入实例在等概率出现的情况下，算法的期望运行时间。
• 最好时间复杂度：在最好情况下，算法的时间复杂度。

一般总是考虑在最坏情况下的时间复杂度，以保证算法的运行时间不会比它更长。

空间复杂度

算法的空间复杂度 $S(n)$ 定义为该算法所耗费的存储空间，它是问题规模 $n$ 的函数。记为

$$S(n)=O(g(n))$$

一个程序在执行时除需要存储空间来存放本身所用的指令、常数、变量和输入数据外，还需 要一些对数据进行操作的工作单元和存储一些为实现计算所需信息的辅助空间。

算法原地工作是指算法所需的辅助空间为常量，即 $O(1)$。

常数阶$O(1)$

常数阶常见于数量与输入数据大小 $n$ 无关的常量、变量、对象。

需要注意的是，在循环中初始化变量或调用函数而占用的内存，在进入下一循环后就会被释放，即不会累积占用空间，空间复杂度仍为$O(1)$。

线性阶$O(n)$

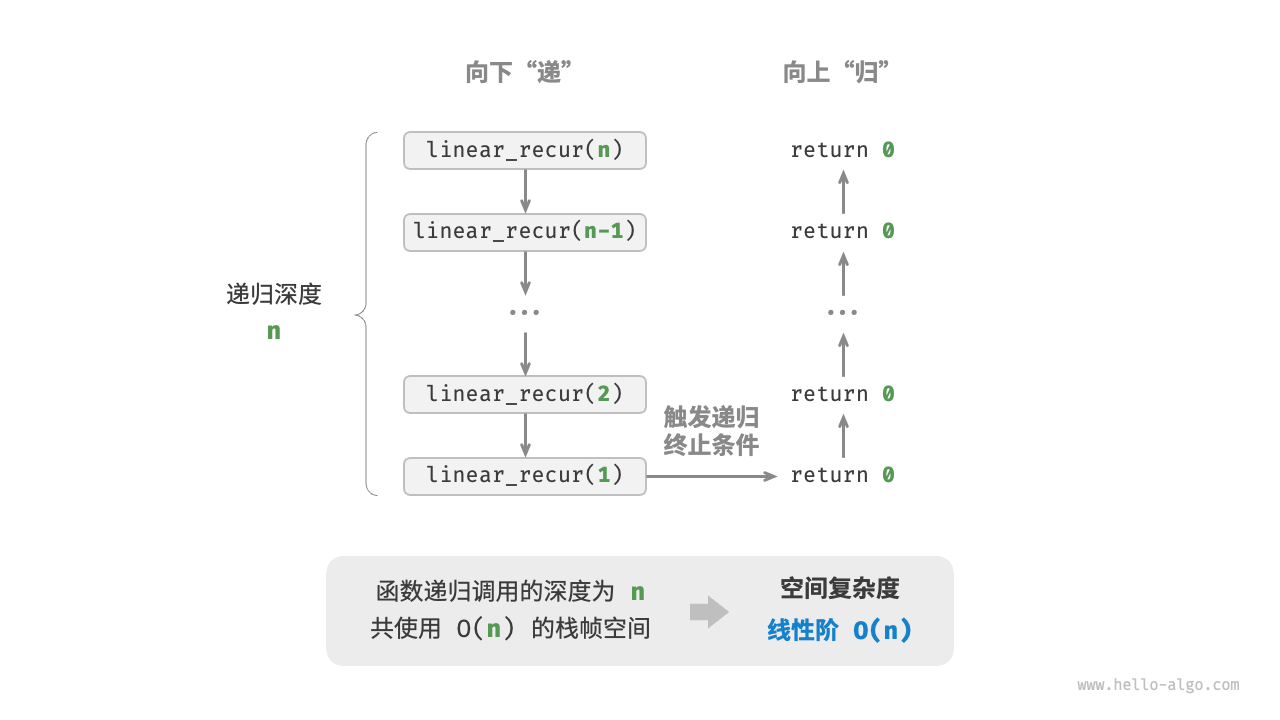
线性阶常见于元素数量与 $n$ 成正比的数组、链表、栈、队列等。

平方阶$O(n^2)$

平方阶常见于矩阵和图，元素数量与 $n$ 成平方关系。

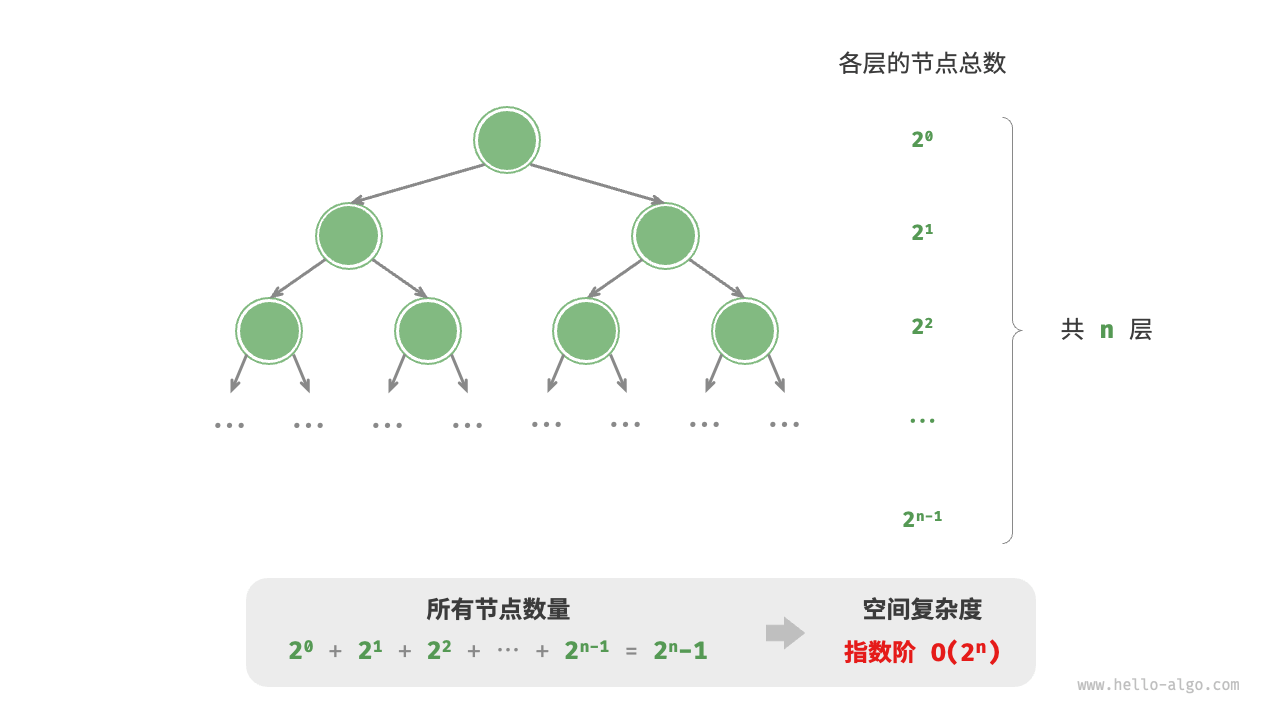
指数阶$O(2^n)$

指数阶常见于二叉树。高度为 $n$ 的「满二叉树」的节点数量为 $2^n-1$ ，占用$O(2^n)$空间。

对数阶 $O(\log (n))$

对数阶常见于分治算法和数据类型转换等。